Title

Combinatoric Derivations and Sidorenko's Conjecture

Daniel Brosch

^{University of Klagenfurt}

March 14, 2024

$$\require{color}$$ $$\definecolor{darkorange}{rgb}{0.8, 0.45, 0}$$

Extremal graph theory

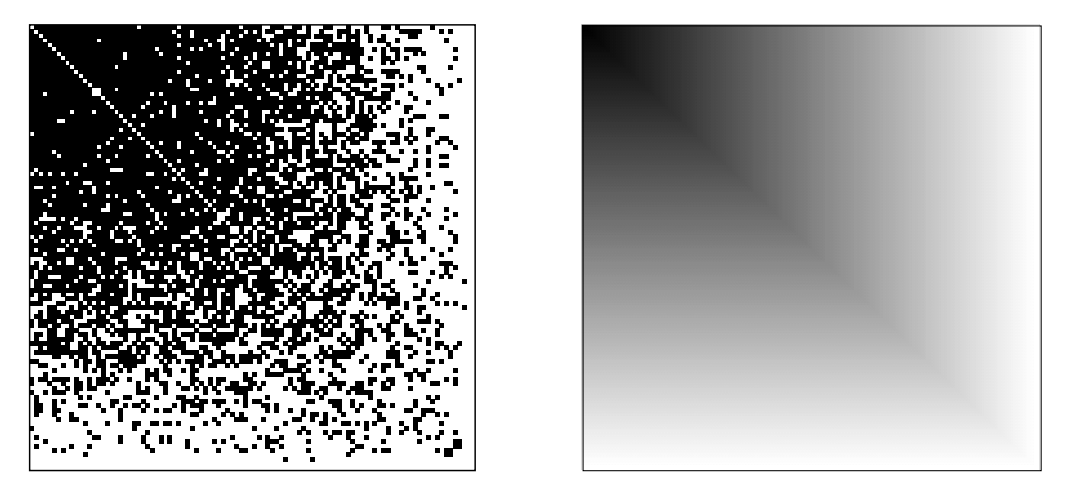
We are interested in limit objects of sequences of graphs $$ \mathcal{G} = (G_i)_{i\geq 0},$$ where $G_i$ is a graph on $i$ vertices.

How many edges can there be in a triangle free graph?

Graphons (Graph-functions)

^{[Lovász, Szegedy, 2006]}

Limits of adjacency matrices: symmetric measurable functions $$W\colon[0,1]^2\to[0,1]$$

Flag Algebras

^{[Razborov, 2007]}

Record only the limits of subgraph densities: $$\phi_{\mathcal{G}}(H) = \lim_{i\to\infty} (\text{density of $H$ in $G_i$}).$$ Flag Algebras consider the relations between different values $\phi_{\mathcal{G}}(H)$ and $\phi_{\mathcal{G}}(H')$.

Subgraph densities

We define the (non-induced) density of a finite graph $\color{darkorange}H$ in $\mathcal{G}$ as $$\phi_{\mathcal{G}}({\color{darkorange}H}):= \lim_{i\to\infty} \text{density of $\color{darkorange}H$ in $G_i$}$$

$$=\lim_{i\to\infty} \mathbb{P}[{\color{green}\sigma_i}({\color{darkorange}H}) \text{ is a subgraph of }G_i ],$$ where ${\color{green}\sigma_i}\colon V({\color{darkorange}H})\to V(G_i)$ is a random injective mapping.

Triangle free graphs

Maximize the edge density in a triangle free sequence $\mathcal{G}$ of graphs of increasing size:

We saw that

but how can we prove an upper bound?

Multiplying subgraph densities

To multiply two subgraph densities, we glue together the graphs:

These relationships are independent of $\mathcal{G}$, motivating the definition

where a graph $H$ now represents the function $$\small H(\mathcal{G}) = \phi_{\mathcal{G}}(H)= \lim_{i\to\infty} \mathbb{P}[\sigma_i(H) \text{ is a subgraph of }G_i].$$

We can fix entries of the $\sigma_i$ to fix (flag) some vertices, and extend the gluing operation to partially labeled graphs (flags):

Formally, we can define flags this way:

Flag Sums-of-Squares

Flags $F$ send graph sequences to real numbers: $$ F (\mathcal{G}) \in [0,1]$$
Then so do real linear combinations of flags
^{The literature calls these Quantum graphs .}
Squares of real numbers are nonnegative:

We can average flags over all choices of labels, unlabeling them:

^{(Razborov calls this the downwards operator.)}

We can now find an upper bound for the edge density in triangle free graphs:

As with polynomial optimization, we can model Flag-SOS using semidefinite programming.

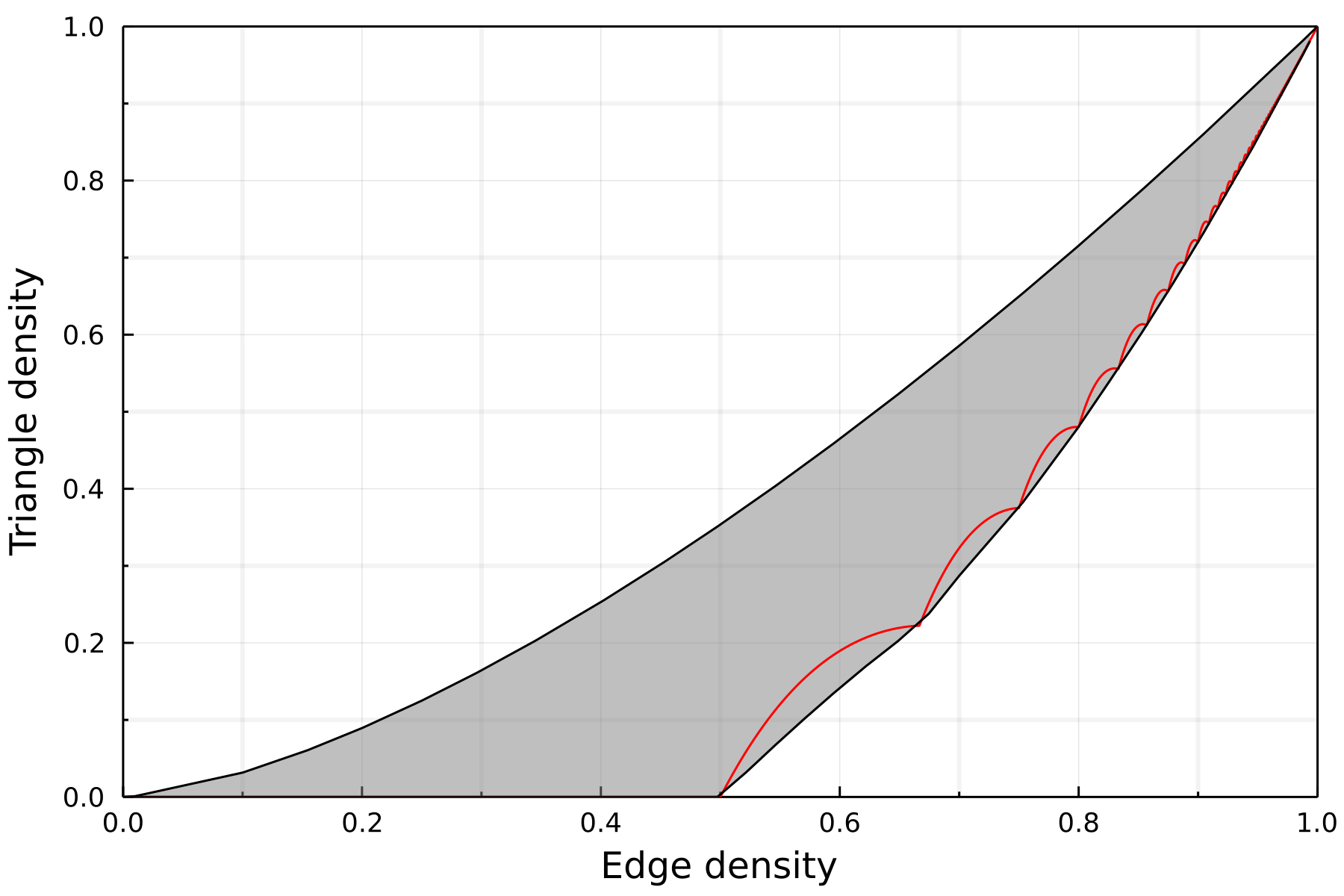
Graph profiles

We saw that triangle free graphs have at most edge density $\frac{1}{2}$.

What happens if we allow some triangles?

Investigating nonnegativity

Let $p=a_1 G_1 + a_2 G_2 + \ldots + a_k G_k$ be a linear combination of unlabeled graphs.

[Lovász, Szegedy 2009]:
If $p\geq 0$, then
$p + \varepsilon$ is a SOS
for any $\varepsilon > 0$.

[Hatami, Norin, 2011]:
The question
"Does $p \geq 0$ hold?"
is undecidable.

Sidorenko's Conjecture

Let $H$ be a bipartite graph, and $\small\rho\in [0,1]$.
Of all the graphs with edge density $\small \rho$, the graph(-limit) obtained by picking edges uniformly at random minimizes the homomorphism density of $H$.

For every bipartite graph $H$,

Progress on Sidorenko's Conjecture

[Mulholland, Smith 1959]: paths

Progress on Sidorenko's Conjecture

[Mulholland, Smith 1959]: paths
[Sidorenko 1991]: trees, even cycles, $K_{n,m}$, bipartite graphs with at most $4$ vertices on one side

Progress on Sidorenko's Conjecture

[Mulholland, Smith 1959]: paths
[Sidorenko 1991]: trees, even cycles, $K_{n,m}$, bipartite graphs with at most $4$ vertices on one side
[Hitomi 2008]: Hypercube graphs, norming graphs

Progress on Sidorenko's Conjecture

[Sidorenko 1991]: trees, even cycles, $K_{n,m}$, bipartite graphs with at most $4$ vertices on one side
[Hitomi 2008]: Hypercube graphs, norming graphs
[Conlon, Fox, Sudakov 2010]:
If one vertex connects to all vertices on the other side

Progress on Sidorenko's Conjecture

[Hitomi 2008]: Hypercube graphs, norming graphs
[Conlon, Fox, Sudakov 2010]:
If one vertex connects to all vertices on the other side
[Sidorenko 1991], [Li, Szegedy 2011], [Kim, Lee, Lee 2013]:
Various recursive constructions

Progress on Sidorenko's Conjecture

[Conlon, Fox, Sudakov 2010]:
If one vertex connects to all vertices on the other side
[Sidorenko 1991], [Li, Szegedy 2011], [Kim, Lee, Lee 2013]:
Various recursive constructions
[Conlon, Lee 2018]: For every bipartite graph $H$ exists a $p$ such that the $p$-blow up of $H$ is Sidorenko.

Progress on Sidorenko's Conjecture

[Sidorenko 1991], [Li, Szegedy 2011], [Kim, Lee, Lee 2013]:
Various recursive constructions
[Conlon, Lee 2018]: For every bipartite graph $H$ exists a $p$ such that the $p$-blow up of $H$ is Sidorenko.
[Blekherman, Raymond, Singh, Thomas 2018]:
$P_3-e^3$ is not a (rational) flag-SOS. The smallest open case $K_{5,5}\setminus C_{10}-e^{15}$ is not a (rational) flag-SOS.

Progress on Sidorenko's Conjecture

[Blekherman, Raymond, Singh, Thomas 2018]:
$P_3-e^3$ is not a (rational) flag-SOS. The smallest open case $K_{5,5}\setminus C_{10}-e^{15}$ is not a (rational) flag-SOS.
[Garg, Raymond, Redlich 2022]: Many cases of Sidorenko's Conjecture cannot be shown using flag-SOS. Most known cases can potentially be recovered using flag-SOS.

Interest for alternative proofs of $P_3-e^3\geq 0$!

The space of graph limits

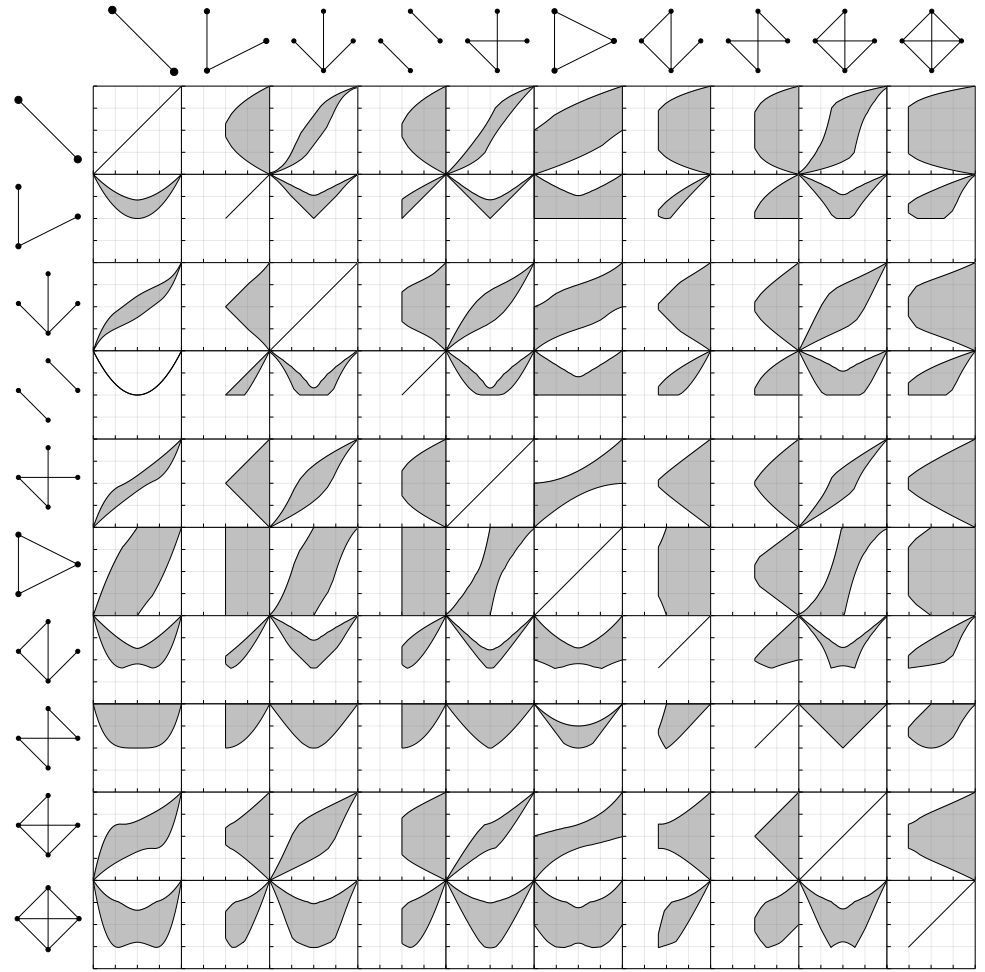
Linear combinations of subgraph densities are continuous functions in this space.
How can we move in the space without leaving it?
Can we define directional derivatives of flags?

Derivatives of flags

[Razborov, 2007] introduces two derivatives:

In direction of deleting a vertex $v$.
In direction of deleting an edge $e$.

Lovász translates the definition to graphons.

Diao, Guillot, Khare, Bajaratnam consider Gateaux derivatives in the space of graphons.

$\partial_{\color{darkorange}v}$: Deleting the vertex ${\color{darkorange}v}$

Usual directional derivatives:

$\partial_{\color{darkorange}v}$: Deleting the vertex ${\color{darkorange}v}$

Usual directional derivatives:

Vertex deletion derivative for flags:

$\partial_{\color{darkorange}v}$: Deleting the vertex ${\color{darkorange}v}$

$$\scriptsize \begin{align*} &(H \text{ density in }(G_{\color{red}i}-{\color{orange}v})) - (H \text{ density in }G_{\color{red}i})\\ & = \mathbb{P}[\sigma_{{\color{red}i}-1}(H)\text{ subgraph of }G_{\color{red}i}-{\color{orange}v}] - \mathbb{P}[\sigma_{\color{red}i}(H)\text{ subgraph of }G_{\color{red}i}] \\ \end{align*} $$

Let $m$ be the number of vertices of $H$. Then we can split the second term: $$\scriptsize \begin{align*} & = \mathbb{P}[\sigma_{\color{red}i}(H)\text{ subgraph of }G_{\color{red}i} \enspace|\enspace v\notin V(\sigma_{\color{red}i}(H)) ] \\ & \quad - \frac{m}{{\color{red}i}} \mathbb{P}[\sigma_{\color{red}i}(H)\text{ subgraph of }G_{\color{red}i} \enspace|\enspace v\in V(\sigma_{\color{red}i}(H)) ] \\ & \quad - (1-\frac{m}{{\color{red}i}}) \mathbb{P}[\sigma_{\color{red}i}(H)\text{ subgraph of }G_{\color{red}i} \enspace|\enspace v\notin V(\sigma_{\color{red}i}(H)) ]\quad \end{align*} $$

Cancelling out terms, we see $$\scriptsize \begin{align*} & = \frac{m}{{\color{red}i}} \mathbb{P}[\sigma_{\color{red}i}(H)\text{ subgraph of }G_{\color{red}i} \enspace|\enspace v\notin V(\sigma_{\color{red}i}(H)) ] \\ & \quad - \frac{m}{{\color{red}i}} \mathbb{P}[\sigma_{\color{red}i}(H)\text{ subgraph of }G_{\color{red}i} \enspace|\enspace v\in V(\sigma_{\color{red}i}(H)) ] \qquad\enspace\\ \end{align*} $$

We can split the first term again to obtain $$\scriptsize \begin{align*} \qquad& = \frac{m}{{\color{red}i}} (1-\frac{m}{{\color{red}i}})\mathbb{P}[\sigma_{\color{red}i}(H)\text{ subgraph of }G_{\color{red}i}] \\ & \quad -\frac{m}{{\color{red}i}} (1+\frac{m}{{\color{red}i}})\mathbb{P}[\sigma_{\color{red}i}(H)\text{ subgraph of }G_{\color{red}i} \enspace|\enspace v\in V(\sigma_{\color{red}i}(H))]. \\ \end{align*} $$

Which can be written in terms of densities again: $$\scriptsize \begin{align*} & = \frac{m}{{\color{red}i}}(H \text{ density in }G_{\color{red}i}) \\ &\quad - \frac{1}{\color{red}i}\sum_{w\in V(H)}(\text{ density of $H$ with vertex $w$ labeled $v$ in }G_{\color{red}i})\\ & \quad + \mathcal{O}\left(\frac{1}{{\color{red}i}^2}\right) \end{align*} $$

$\partial_{\color{darkorange}v}$: Deleting the vertex ${\color{darkorange}v}$

Vertex deletion derivative for flags:

$\partial_{\color{darkorange}e}$: Deleting the edge ${\color{darkorange}e}$

Interpretation as Lie-Derivations

The (symmetrized) edge-deletion derivative $[\hspace{-0.15em}[\partial_e]\hspace{-0.15em}]$ is the derivation along the flow

How to actually "move" in a direction?

If $\partial_{\color{darkorange}v}(f)(\mathcal{G}) < 0$, can we actually find a new graph limit $\mathcal{G}'$ with $f(\mathcal{G}') < f(\mathcal{G})$?

Problem: We can only delete a vertex ${\color{darkorange}v}$ (or edge) once. In a graph limit, deleting one vertex does not shift its subgraph densities!

Solution: We instead assume that $\partial_{\color{darkorange}v}(f)(\mathcal{G}) < 0$ for a positive fraction of vertices $v$. We can then (very carefully) pick a subset of these to delete.

Using the derivatives in optimization

Let ${\color{darkorange}f}$ be a linear combination of subgraph densities, with minimizer $\mathcal{G}$ .

Then $\partial_{\color{red}v} {\color{darkorange}f}(\mathcal{G}) = 0$ for nearly all vertices ${\color{red}v}$.
Then $\partial_{\color{red}e} {\color{darkorange}f}(\mathcal{G}) \geq 0$ for nearly all edges ${\color{red}e}$.

We can add additional constraints to optimization problems!

We do not need to assume that we are in the interior of the profile.

Using the derivatives in optimization

$$ \begin{align} \min_{\mathcal{G}}\enspace {\color{darkorange}f}(\mathcal{G}) = \min_{\mathcal{G}}\enspace& {\color{darkorange}f}(\mathcal{G})\\ \text{s.t. }& \mathbb{P}[\partial_{\color{red}v} {\color{darkorange}f}(\mathcal{G}) = 0]=1, \\ & \mathbb{P}[\partial_{\color{red}e} {\color{darkorange}f}(\mathcal{G}) \geq 0]=1. \end{align} $$

We can find better SOS certificates in the quadratic module generated by these constraints.

Proof idea

Assume there is an $\varepsilon$-subset of vertices/edges that violate the constraints.
Show that there exists a subset of $\Theta(n)$ vertices resp. $\Theta(n^2)$ edges we can remove consecutively to shift the objective.

Problem: We have to pick the elements "independently enough".
Otherwise we cannot guarantee that after removing some vertices, the derivatives of the remaining vertices do not change their sign.

The proof for edge-deletion

^{(based on Razborov's proof, translated to non-induced setting)}

Lets assume we have found an "improving direction", i.e. $$\mathbb{P}[\partial_e f(\mathcal{G}) < 0]> 0.$$
Then there exist constants $\varepsilon, \varepsilon'> 0$ independent of $n$ with $$ \mathbb{P}[\partial_e f(G_n) < -\varepsilon]> \varepsilon' $$ for $n$ big enough.
Define the set of bad edges as $$ \mathrm{Bad} := \{e \in E(G_n) \enspace\vert\enspace \partial_ef(G_n) \leq -\varepsilon\}.$$
We need to make sure not to pick too many edges adjacent to the same vertex. For this, we sample a random set $V\subset V(G_n)$ of vertices uniformly at random of size $$|V| = \left\lfloor \sqrt{\delta}n+1\right\rfloor,$$ where $\delta > 0$ is a small enough constant (see later) independent of $n$.
Let $$ \mathrm{Bad}\vert_V := \mathrm{Bad} \cap \binom{V}{2}$$ be the set of bad edges with both vertices in $V$. Then we can upper bound $$\left\vert\mathrm{Bad}\vert_V \right\vert \leq \binom{\left\lfloor \sqrt{\delta}n+1\right\rfloor}{2} \leq \delta n^2$$ if $n$ is big enough.
We find a lower bound $$ \mathbb{E}\left\lbrack \left\vert\mathrm{Bad}\vert_V \right\vert \right\rbrack \geq \varepsilon'\binom{\left\lfloor \sqrt{\delta}n+1\right\rfloor}{2} \geq \varepsilon' \frac{\delta n^2}{2},$$ which allows us to fix a subset $V_n$ of size $\Theta(n^2)$ for each $n$ (big enough) such that $$\varepsilon'\frac{\delta n^2}{2} \leq \left\vert\mathrm{Bad}\vert_{V_n} \right\vert \leq \delta n^2.$$
We arbitrarily fix the order of elements of each chosen set of edges $$\mathrm{Bad}\vert_{V_n} = \{e_1,\dots, e_{m_n}\}, $$ where $m_n := \left\vert\mathrm{Bad}\vert_{V_n} \right\vert = \Theta(n^2)$.
We now want to remove the edges in this order. Let $$G_{n,i} := G_n - \{e_1, \ldots, e_i\}.$$
Then we can show we have \begin{align*}\small f(G_{n, m_n}) - f(G_n) & = \sum_{i=1}^{m_n}\left(f(G_{n,i}) - f(G_{n,i-1})\right) \\ & = \frac{1}{n(n-1)}\sum_{i=1}^{m_n} (\partial_{e_i}f)(G_{n,i-1}). \\ \end{align*}
Because of the randomized construction, we can estimate the difference $$|(\partial_{e_i} f)(G_{n,i-1}) - (\partial_{e_i} f)(G_{n})| = \mathcal{O}(\sqrt{\delta}),$$ as we modify $G_n$ on at most $|V| = \left\lfloor \sqrt{\delta}n+1\right\rfloor$ vertices.
Since $m_n\leq \delta n^2$, we bound \begin{align*}\small p(G_{n, m_n}, f) - p(G_n, f) & = \frac{1}{n(n-1)}\sum_{i=1}^{m_n} (\partial_{e_i})(G_{n}) \pm \mathcal{O}(\delta^{3/2}) \\ & \leq -\frac{1}{n(n-1)}\frac{\varepsilon\varepsilon'\delta n^2}{2} \pm \mathcal{O}(\delta^{3/2}) \\ & \leq -\frac{\varepsilon\varepsilon'\delta}{4}, \end{align*} for $\delta$ small enough and $n$ big enough.
By compactness of the space of graph limits, we can choose a converging subsequence $\tilde{\mathcal{G}}$ of $(G_{n,m_n})_{n>0}$, for which $f$ has a smaller value: \begin{align*}\small f(\tilde{\mathcal{G}}) - f(\mathcal{G}) = \lim_{n\to\infty}p(G_{n,m_n}, f) - p(G_n, f) \leq -\frac{\varepsilon\varepsilon'\delta}{4} < 0, \end{align*} contradicting the assumption that $\mathcal{G}$ minimizes $f$.

Main contribution

We show that the proofs generalize to more complicated actions on three or more vertices.

The resulting functions are derivations of the flag algebra (i.e. Leibniz's rule holds).

Main observation: We only ever need to apply the operation $\Theta(n^2)$ times! We can construct still "independent" sets probabilistically.

Hinge-switch derivative

We define the derivative $\partial_{\text{hinge}}$ based on the operation on vertices $i,j,k$, which swaps the edges $\{i,j\}$ and $\{i,k\}$.

Edge-swap derivative

We define the derivative $\partial_{\text{swap}}$ based on the operation on vertices $i,j,k, l$, which swaps the edges $\{i,j\}$ and $\{k,l\}$.

And many more complicated ones! For example, we can blow up vertices, invert directed edges, connect vertices to all others...

SOS based proofs for small cases of Sidorenko's

We found an exact (and easily human checkable) flag-SOS certificate for \begin{align} 0 = \min\enspace& P_3 - e^3\\ \text{s.t. }& \mathbb{P}[\partial_{\text{swap}}(P_3 - e^3) \geq 0 ]=1 \end{align} Where

We also found numeric certificates for the two next bigger cases with no "pure" flag-SOS based proof.

SOS-based proof of $P_3-e^3\geq 0$

In a minimizer, we have

Questions:

Conic combinations of combinatoric derivations are again combinatoric, by applying the combined operations a number of times at the correct ratios. How does this convex cone look like?
Especially, what are the extreme rays of the cone of combinatoric derivations? For example: $$\partial_{\text{invert edge $e$}} = \partial_{\text{add edge $e$}} + \partial_{\text{delete edge $e$}},$$ so $\partial_{\text{invert edge $e$}}$ is not an extreme ray.
What does the Lie-bracket tell us here? When is $[\partial_f, \partial_g]$ again a combinatoric derivation?
Adding all derivations to a problem, can we then solve it exactly with SOS-methods?

Software:

Julia package implementing multiple symmetry reduced flag-SOS hierarchies for arbitrary Flags:
https://github.com/DanielBrosch/FlagSOS.jl


        pkg> add FlagSOS

The package also supports non-asymptotic problems, and problems that are not combinatoric (e.g. SOS for (multi-)symmetric functions in $n$ variables).

Paper:

Very much work in progress. Other work related to flag algebras is in my thesis.